
Since I encountered an essay by A. K. Dewdney over ten years ago,
somewhat I had been obsessed about mechanical implementation of
boolean logic. The essay introduced ideas of kinetic binary
calculator as an imaginary story of ancient civilization. This
fantastic tale attracted me, and my theme at the art college became
how to make a computer made from wood.
Last year, my boss gave me a Dewdney's book "The Tinkertoy
Computer and Other Machinations", which includes the essay, and my
enthusiasm came back. I made a couple of prototypes to realize
boolean logic without electronics. This is the latest attempt.
I chose a half adder as the motive because half adders are used
everywhere in a computer hardware, and it seems nice complexity for
the project. I thought this is the best example to show the idea
that computer's concept is independent with hardware. In other
words, I wanted to prove that computer is purely conceptual entity
and you can make it from any material besides electronics parts.
I first built a wooden AND operator. Can you tell how this toy
work? The top two holes show the input, and the center hole shows
the answer. Background board shows two kind of state T (True) and F
(False). Because of gravity, initial state is T AND T = T, once you
pull one of bars up, the center piece is also pulled up, and the
answer becomes F. This is how AND works.
Basically, any boolean logic can be possible with AND, and
another operator NOT (even OR can be constructed from AND and NOT).
Let's think about a half adder. A half adder is a primitive adder
and you can only add two bits. There are only four positions.
- 0 + 0 = 0 0
- 0 + 1 = 0 1
- 1 + 0 = 0 1
- 1 + 1 = 1 0
Let the inputs A and B, and the outputs S (sum, the low bit) and
C (carry, the high bit). A half adder can be shown two boolean
equations from AND(∧) and NOT(¬).
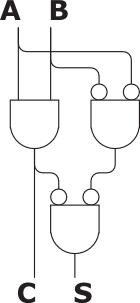
- C = A ∧ B
- S = A xor B = ¬(A ∧ B) ∧ ¬(¬ A ∧
¬B)
Finally, I constructed parts along with this formula. I used
gears as NOT operator.
 |
 |
 |
 |
| 1 + 1 = 1 0 |
1 + 0 = 0 1 |
0 + 1 = 0 1 |
0 + 0 = 0 0 |








